Astronomía Digital

Astronomía Digital es la primera publicación electrónica de distribución gratuita en español orientada a la astronomía aficionada.

Todos los contenidos están disponibles de forma libre y completos en la Red para su lectura. Además, puedes leernos en papel imprimiéndonos gracias al formato PDF.

Astronomía Digital quiere llegar a todos los rincones de nuestro planeta donde se hable español.

Inicio > Índice nº 11 > Artículos

Luis Salas López | Círculo Científico de Canarias

¿Cual es la escala que utilizan los astrónomos para medir el brillo de las estrellas? Aprende a utilizar las magnitudes con una hoja de cálculo.

	magnitudes.xls (Excel)
	magnitudes.sxc (OpenOfice.org)

La escala al revés

El primer tropezón

La escala de la magnitud estelar, es uno de los primeros tropiezos con los que se encuentra la persona que se interesa por la astronomía. Y esto es así porque al novicio lo primero que le cuesta entender es que la "escala está al revés". Es decir, los números más grandes corresponden con una cantidad de luz menor, lo que entra en contradicción con el uso y las buenas costumbres del resto de las escalas de pesos y medidas que usamos.

Esto es un problema no sólo para los novatos, sino para el buen entendimiento entre los más expertos aficionados a la astronomía. ¿Por qué se puede afirmar esto? Pues muy fácil. Es frecuente el problema de comunicación que ocurre entre aficionadas cuando comentan "la estrella variable tal está subiendo". Siempre hay alguien que pregunta "Pero qué ha subido el brillo o la magnitud". Y es que, claro, que suba el brillo es lo contrario de que suba la magnitud. Así pues, hay aclarar bien de a qué concepto se refieren. Este tipo de preguntas no ocurren en otras escalas de la vida. Si sube el IPC, el caudal de un río, o si aumenta el volumen, el peso, o el plazo de cualquier cosa, no tenemos problemas para saber a que se refieren.

El culpable

Bueno, aclaremos. La culpa la tiene Hiparcos (120 AC) a quien se le ocurrió la sencilla idea de que las estrellas más brillantes son de primera magnitud. Esto tiene cierta lógica pues así se enfatiza que las más brillantes son las más importantes. Hiparcos denominó a las estrellas un poco menos brillantes, como estrellas de segunda magnitud. Y así sucesivamente hasta las estrellas que apenas podía ver a simple vista que las llamó de sexta magnitud.

Esta clasificación fue utilizada por posteriores astrónomos, consolidando de esta forma su uso. Y precisamente con el uso del telescopio se descubrieron estrellas más débiles que las de sexta magnitud, Estas estrellas, más débiles que las visibles a simple vista, tuvieron que clasificarse como de séptima magnitud. Algo parecido sucedió con las siguientes estrellas más débiles, las de octava magnitud, novena magnitud, y así... hasta nuestros días. Con unos prismáticos se pueden ver estrellas tan débiles como las de magnitud 10. Con un telescopio de aficionado, estrellas de magnitud 14. Con uno profesional se llega a magnitud 20 y 25. Y con el Hubble se puede llegar a estrellas de magnitud 30.

¡Incluso bajo cero!

En tiempos recientes, se observó que algunas estrellas (muy pocas) eran en realidad más brillantes que las de primera magnitud, y por tanto se las clasificó de magnitud cero. Pero podemos extender esa escala, no sólo a las estrellas, sino también a los planetas. Como algunos de ellos se ven mucho más brillantes que cualquier estrella de magnitud uno, e incluso de magnitud cero, se puede decir que planetas como Marte, Júpiter y, sobre todo, Venus tienen magnitudes negativas. De hecho, Venus tiene magnitud -4. Si seguimos con esta escala, tendríamos que situar a la Luna llena, que brilla mucho más que Venus, con la magnitud -12. Y, por tanto el Sol le correspondería magnitud -27.

En resumen, cuando la magnitud de una estrella es un número grande, se indica que es muy débil. Y al contrario, una estrella con magnitud baja, cero, e ¡incluso negativa!, es muy brillante.

Y además logarítmica

La escala de magnitudes aparte de estar al revés, también es logarítmica, (para mayor sufrimiento de los aficionados).

2º Culpable: la sensibilidad

Ya en el siglo XIX, los astrónomos fueron conscientes de que hacía falta un método más preciso que el ojo de buen cubero para asignar magnitudes. Y precisamente hablar de ojos nos viene muy a cuento. Los ojos, al igual que el oído o el tacto, no tienen una sensibilidad proporcional al estímulo, sino que todos los sentidos intentan ser muy sensibles a los estímulos muy débiles y en cambio ser muy toscos, burdos o poco sensibles a los estímulos muy fuertes.

El tacto, millonario

Por ejemplo, en la piel podemos sentir el roce suave de una pluma, el caer de un clip o una grapa. Es interesante, y necesario para la supervivencia, percibir el más leve roce o presión. Pero si esa sensibilidad fuese proporcional, con un estimulo 1000 veces superior, deberíamos sentir un dolor inaguantable. En cambio, la forma en que nuestra piel funciona, es que cuanto más fuerte es la presión más insensible nos hacemos a ella. Así, si ponemos sobre la mano una caja con 1000 grapas (unos 30 gramos), notaremos una ligera presión. Habría que poner sobre nuestra mano no una, sino 1000 cajas, que hacen un peso de unos 30 Kg., para perder la sensación de tacto y comenzar a percibir el dolor. Es decir, el tacto puede percibir desde una presión muy débil a otra un millón de veces más fuerte.

El oído, billonario

Algo parecido ocurre con el oído. Podemos apreciar el más leve susurro de la brisa o de las hojas de los árboles, pero no nos quedamos sordos al hablar nosotros mismos o al escuchar a otra persona, a pesar de que la intensidad sonora es un millón de veces superior. Podemos incluso soportar el ruido del tráfico o el despegue de aviones que producen una intensidad sonora ¡un billón! de veces más fuerte que el de las hojas de los árboles, ¡y sin quedarnos sordos!. La sensibilidad del oído abarca desde el sonido más débil, que puede percibirse hasta uno un billón de veces superior. Estas diferencias tan abismales, de 1 a un billón, hacen difícil de manejar y comparar los sonidos y los ruidos. Por tanto, interesa transformar esa escala en otra más manejable.

La intensidad sonora se mide en una escala logarítmica conocida: los decibelios. En esta escala, los belios, equivale a contar el número de ceros de una cifra. Una cantidad de 10, al tener un cero, equivale a 1 belio, mientras que 1000000 (un millón), con sus seis ceros, equivale a 6 belios. En cambio, los decibelios, (décima parte de un belio), cuentan también el número de ceros de una cantidad pero multiplicada por 10. Por ejemplo, 1000, como tiene 3 ceros, correspondería a 3 belios, pero en decibelios sería diez veces más. Por tanto, 1000 equivale a 30 db. Un millón, como tiene 6 ceros, corresponde a 60 decibelios. Y un billón, que es difícil de manejar, como tiene 12 ceros equivale a 120 decibelios.

Algunas referencias para concretar: El oído puede percibir sonidos tan débiles como unos pocos decibelios. Una conversación normal tiene unos 60 db. Y un sonido de más de 120 db nos produce dolor.

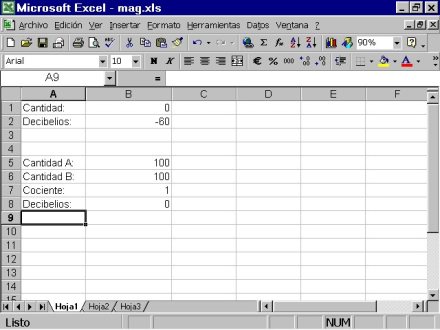
Ejemplo 1 y 2.

Entiéndelo mejor con hoja de cálculo

Ejemplo 1: Podemos utilizar la hoja de cálculo para probar estos casos y así poder entender mejor las escalas logarítmicas. Abrimos el programa (por ejemplo, Excel de Microsoft o Calc de OpenOffice), y en una hoja de cálculo nueva, ponemos en la celda A1 el rótulo "Cantidad:", y en A2 el rótulo "Decibelios:". De momento en la celda B1, escribiremos la cantidad "1000", y en la celda B2 teclearemos una fórmula para que nos dé los decibelios equivalentes a la cantidad que especificaremos en B1. Todas las fórmulas en Excel y Calc tienen que empezar por el signo "=", así que en B2 escribimos "=10*log10(B1)", todo seguido sin espacios.

Al pulsar ENTER, debería salir el número 30, que indica que una cantidad de 1000 equivale a 30 db. Cambia en número 1000 por 100, y verás que corresponde a 20 db. Si pones una cantidad de 1.000.000.000.000 (un billón) le corresponde 120 db, que es lo máximo que aguanta el oído sin dolor.

Nota: La función LOG10() es una función que da el logaritmo en base 10 de lo que esté entre paréntesis.

Vamos a probar con cantidades menores que la unidad. Si en la celda B1 ponemos "0,1", veremos que corresponde a -10 db, y si introducimos una millonésima, es decir "0,000001", comprobaremos que equivale a -60 db. Por tanto una décima, al tener un decimal, cuenta como -10 db, pero una millonésima al tener 6 decimales equivale a -60 db.

Resumiendo: las cifras mayores que 1 tienen db positivos y las menores que 1 tienen db negativos. Los decibelios vienen a ser el número de ceros (si cantidad> 1) o de decimales (si cantidad < 1) multiplicado por 10.

Nota: No se pueden poner cantidades negativas. Prueba y verás que aparece error en la celda B2.

Entiéndelo mejor con hoja de cálculo

Ejemplo 2: En realidad, el ejemplo anterior está muy simplificado. Siendo más estrictos el número de decibelios nos indica cuánto más fuerte es una señal o sonido respecto a otro. Observa que para calcular los decibelios siempre hay que comparar un sonido con otro: no hay un valor cero de referencia que indique que la señal o sonido es nulo. Por la misma razón no se puede calcular los decibelios de una cantidad negativa. Las proporciones son siempre positivas. Estas son propiedades características de todas las escalas logarítmicas.

Volviendo al programa, escribiremos en la celda A5 el rótulo "Cantidad A:", en A6 "Cantidad B:". En A7 "Cociente:", y en A8 "Decibelios:". Después de estos rótulos vamos a poner los datos. Por ejemplo, en la celda B5, la cantidad 1000, y en B6 un 10. En B7 introducimos la fórmula que nos dé la proporción entre una cantidad y otra, osea "=B5/B6". Al pulsar ENTER, saldrá 100, pues 1000 es 100 veces mayor que 10. Ahora en la celda B8 tecleamos la formula "=10*log10(B7)".

Al pulsar ENTER da como resultado 20 db. Esto quiere decir que A es 20 decibelios mayor que B. Y esto es correcto pues la cantidad A es 100 veces mayor que la B, y el factor 100 equivale a 20 db según vimos anteriormente. Si ponemos en B5 la cantidad 10.000.000 (diez millones), nos da que A (diez millones) es 60 db más fuerte que B (diez). ¿Qué pasa si ponemos las cantidades al revés?, Pues si cambiamos la cantidad A a 10 y la B a 10.000.000, ahora nos sale -60db. Es decir, A es 60 db más débil que B, lo que equivale a decir que A es un millón de veces más débil que B..

Antes decíamos que no había un valor cero de referencia. Si en B5 escribimos "100" y la misma cifra la ponemos en B6, veremos que al ser las dos cantidades iguales, el cociente es 1, que equivale a 0 db. Cuando tenemos 0 db no estamos diciendo que no hay sonido, sólo estamos diciendo que 0 db es equivalente a 1, osea que una cantidad es igual que otra.

El ojo, 13 veces billonario

¿Y qué pasa con el ojo?. Algo parecido. El ojo se adapta asombrosamente bien a condiciones de luz tan cambiantes como la noche estrellada sin luna, o un día cegador de verano con el Sol resplandeciente en lo alto. ¿Cómo lo hace?, Los aficionados a la astronomía conocemos bien los dos mecanismos. Uno de ellos, el que se adapta más rápido, es el de agrandar (o disminuir) la abertura de la pupila, relajando o contrayendo el iris. El otro mecanismo es más lento, pues consigue un aumento o disminución de la sensibilidad a la luz, cambiando la química de la retina.

Respecto al primer mecanismo, está muy extendido un mal uso de este vocabulario, pues se dice que la pupila se dilata, cuando en realidad es el iris el que se relaja. La pupila es sólo el hueco que deja el iris para que pase la luz. La pupila es pasiva, el iris es la parte activa. Este método es muy rápido ya que simplemente hay que mandar una señal nerviosa a los músculos del iris, y éstos reaccionan en décimas de segundo. Pero sólo adapta la sensibilidad a la luz en un factor de 20, que es la consecuencia de abrir la pupila a su máximo diámetro, (unos 7 mm), o cerrarla (hasta un mínimo de unos 2 mm). Viene muy bien durante el día, para las múltiples ocasiones en que pasamos de un ambiente a otro con diferente grado de iluminación, o si miramos un objeto a la luz del sol, o a la sombra.

El segundo método, aunque mucho más lento (15 minutos de adaptación), es el que hace el gran ajuste de la sensibilidad a la luz en condiciones extremas. Va ajustándose poco a poco a lo largo de las horas del día. Nos permite ver perfectamente a la luz del Sol, al igual que más tarde, durante su puesta, para terminar adaptándose a la noche en la que podemos ver casi sin luz. Este solución puede ajustar la sensibilidad a la luz en un factor de un billón.

A los fotógrafos les vendrá muy bien la siguiente analogía: El método que utiliza los músculos del iris equivale a ajustar el diafragma del objetivo desde f:5 a f:17. Por el contrario, el método que modifica la química de la retina se parece a cambiar la química de la película fotográfica, es decir, a modificar su ASA. Sólo que el ASA debería variar de ASA uno hasta ASA un billón.

El ojo, además de esta magnifica capacidad de adaptación, funciona de forma parecida al tacto y al oído, también es logarítmico. Ya en el siglo XIX, se observó que en la escala de Hiparcos, entre una magnitud y otra había una proporción real aproximadamente de 2,5. Si vemos una estrella A de magnitud 2 y otra B de magnitud 3, en realidad A es unas 2,5 veces más brillante que B. De esta manera, 2 magnitudes corresponde, aproximadamente a una diferencia de 2,5 x 2,5 = 6,25. Lo que quiere decir que en el caso de dos estrellas de magnitudes 1 y 3, la de magnitud 1 es en realidad 6,25 veces más brillante que la de magnitud 3. A una diferencia de 3 magnitudes le corresponde 2,5 · 2,5 · 2,5 = 15,625, y así sucesivamente.

Entiéndelo mejor con hoja de cálculo

Ejemplo 3: En la parte inferior de la hoja de cálculo verás unas etiquetas señaladas como hoja1, hoja2, hoja3. Haz clic en la hoja2 para crear en ella una tabla que nos de la correspondencia aproximada entre diferencias de magnitudes y las diferencias de brillo reales. En la celda A1 escribimos "Dif Mag" para indicar la diferencia de magnitud. En B1 "Dif Bri Real" para rotular la diferencia de brillo real. En la celda A2 introducimos la cantidad "1", en A3 un "2". Ahora vamos a realizar una técnica llamada "llenado automático" que utilizaremos a menudo. Primero seleccionamos la celda A2 y la A3. Las dos deben quedar dentro de un borde negro. Si ahora te fijas en la esquina inferior derecha de este borde negro veras un cuadradito que se llama precisamente "llenado automático", si señalas con el ratón en él, el puntero se transforma en una cruz negra pequeña. Pues en esa situación arrastra el ratón hacia abajo hasta la fila 35, y se genera una serie que va desde el 1 hasta el 34 sin tener que escribirla. Por último en la celda B2 introduciremos la fórmula "=2,5^(A2)". Fíjate que usamos el acento circunflejo ^, que está a la derecha de la tecla P. Los paréntesis en realidad no son necesarios pero es para forzar que el acento circunflejo no acentúe la letra A. Esta fórmula viene a decir que el número 2,5 lo elevamos a lo que haya en la celda A2. Si pulsas ENTER, debe salir precisamente el número 2,5. Ahora sólo falta usar otra vez la técnica de llenado automático. Haz clic en la celda B2 y observa su borde negro. De nuevo en su esquina inferior aparece el cuadradito de llenado automático. Señálalo y arrástralo como antes hasta la fila 35.

Ya tenemos una tabla que nos muestra la correspondencia aproximada entre diferencias de magnitudes y proporciones reales de brillo. Comprueba que una diferencia de dos magnitudes equivale a un factor de brillo de 6,25, pero tres magnitudes corresponde a un factor de brillo de 15,625. Curiosamente cinco magnitudes equivale casi a un factor de 100. Es decir una estrella que tenga 5 magnitudes más que otra es en realidad 100 veces más débil.

La Luna llena tiene magnitud -12, por tanto si la comparamos con una estrella débil de sexta magnitud, hay una diferencia de magnitudes de 18, (12 + 6). Si comprobamos en la tabla, una diferencia de 18 magnitudes equivale a 14 millones de veces más brillante. Dicho de otra manera, si en el cielo pusiéramos 14 millones de estrellas de magnitud 6, darían tanta luz como la Luna llena.

De la misma forma vemos que el Sol, que tiene magnitud -27, es 33 magnitudes (27 + 6) más brillante que una estrella de magnitud 6. Pero en la tabla, 33 magnitudes equivalen a 1,35E+13 que es la forma científica de un 1 seguido de 13 ceros, o también un 13 seguido de 12 ceros, es decir, 13 billones. Por tanto, si durante la noche vemos una estrella tan débil como de magnitud 6, y al día siguiente miramos al Sol, quiere decir que nuestros ojos tienen una capacidad de adaptarse y ver, en dos condiciones de luz tan dispares como 13 billones de veces más brillante una que otra. El ojo es 13 billonario.

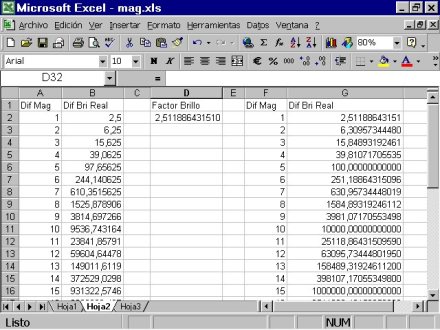
Ejemplos 3, 4 y 5.

Y también caprichosa

100 es más redondo que 97,6

Como decíamos anteriormente, en el siglo XIX, se pretendía establecer una escala bien determinada de magnitudes y que se ajustara bastante a la escala de Hiparcos, ya universalmente aceptada, pero no bien definida. Si de una magnitud a otra hay una proporción de brillo real de 2,5 veces, una diferencia de 5 magnitudes equivale a 2,5⁵ = 97,6 veces. A un astrónomo de Oxford llamado Norman R. Pogson, en 1856, se le ocurrió redefinir la nueva escala proponiendo que una estrella con 5 magnitudes más que otra, sería exactamente 100 veces más débil. Esto obligaba a cambiar el factor de 2,5 para que al elevarlo a la quinta potencia nos diera el número 100. En plan matemático, había que calcular un nuevo factor x tal que x⁵ = 100. Una vez resuelto da

Entiéndelo mejor con hoja de cálculo

Ejemplo 4: En la hoja2 que utilizamos para el ejemplo anterior vamos a calcular de forma más precisa el valor de 2,512 que indica cuantas veces es más brillante una estrella cada vez que le añadimos una magnitud. En la celda D1 escribimos el rótulo: "Factor Brillo", y en D2 introduciremos la fórmula "=100^(1/5)", (elevar algo a 1/5 es como hallar su raíz quinta).

Al pulsar ENTER te dará el resultado 2,51188643 que es más preciso que el anterior. Si vas señalando con el ratón en los botones de la derecha de la barra de herramientas formato encontrarás un botón que dice "Aumentar decimales". Púlsalo varias veces y verás este factor con mayor precisión. Como sospechas es un número con infinitas cifras decimales.

Quedaba así definida de forma exacta la nueva escala. Cada vez que nos movamos 5 magnitudes por la escala multiplicaremos o dividiremos por 100 el brillo real. Una estrella 10 magnitudes más débil que otra sería justamente 100 · 100 = 10.000 veces menos brillante. Si diferencia entre dos estrellas es de 15 magnitudes significa que una estrella es exactamente 100 · 100 · 100 veces más brillante que la otra. ¿A qué diferencia de brillo real equivale una diferencia de 30 magnitudes? Hmmm, exacto, justamente a un millón.

Entiéndelo mejor con hoja de cálculo

Ejemplo 5: Vamos a repetir la tabla que hemos hecho en el ejemplo 3, pero esta vez con el valor real del factor de brillo que hemos calculado en el ejemplo 4. Así tendremos la correspondencia exacta entre diferencias de magnitudes y las diferencias de brillo reales. En la celda F1 escribimos "Dif Mag". En la celda G1 ponemos "Dif Bri Real" para indicar esta vez la diferencia de brillo real y exacto. En la celda F2 ponemos la cantidad "1", en la F3 la cantidad "2", seleccionamos la celda F2 y la F3. Las dos quedarán dentro de un borde negro. Señalamos con el ratón en el cuadradito de llenado automático y arrastramos hasta la fila 35, generando la serie del 1 hasta el 34. En la celda G2 introducimos la fórmula "=D$2^F2". Al dar al ENTER, saldrá el número 2,51188643. Hacemos clic en la misma celda G2 y de nuevo cogiendo su esquina inferior hacemos llenado automático hasta la fila 35. Si en algunas celdas sale "#####" es que tienes que hacer más ancha la columna G, o bien disminuir el número de decimales.

Y ahora ya tenemos la tabla de equivalencias exactas entre diferencias de magnitudes y diferencias reales de brillo. Fíjate que cada cinco magnitudes, el brillo corresponde a números redondos. Puedes comparar esta tabla con la otra. Sólo para diferencias de magnitudes muy grandes, la diferencia es apreciable.

Generalizando

Ya sabemos como funcionan las escalas logarítmicas, y en concreto cómo funciona la escala de magnitud estelar. Podríamos generalizar nuestro conocimiento. Hasta ahora sabemos la diferencia de brillo real que hay entre dos estrellas de magnitud conocida, pero sólo de magnitudes enteras, como magnitud 3 ó 4. Pero en realidad hay estrellas que tienen un brillo intermedio entre estrellas de magnitud 3 y estrellas de magnitud 4. Por tanto esas estrellas tendrán que tener magnitudes con números decimales. Si tenemos una estrella de magnitud 2,7 y otra de magnitud 3,4 ¿cuántas veces es más brillante la primera que la segunda?. Pues tendremos que restar sus magnitudes y elevar 2,512 al resultado de esta diferencia. La fórmula matemática sería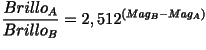

El cociente de los brillos es igual al factor de brillo elevado a las diferencias de magnitudes.

Entiéndelo mejor con hoja de cálculo

Ejemplo 6: Vamos a utilizar esta vez la hoja3. Comenzamos por los rótulos. En la celda A1 ponemos "Mag A", en A2 escribimos "Mag B", en A3 "Dif Mag", en A5 "Brillo de A es", en C5 "veces el brillo de B". Ahora le toca el turno a los datos, en B1 ponemos 2,7, en B2 ponemos 3,4. Por último las fórmulas: en B3 escribimos "=B2-B1", y en B5 ponemos "=2,512^B3".

Al dar ENTER tendremos que el brillo de A es 1,9 veces el brillo de B. Si ponemos que la magnitud de A es 1 y la de B es 6, por tanto A es 5 magnitudes más brillante que B, veremos que sale que el brillo de A es 100 veces el brillo de B. Si lo hacemos al revés, y ponemos que la magnitud de A es 6 y la de B es 1, ahora tenemos que A es 5 magnitudes más débil que B, y veremos que el resultado dice que el brillo de A es 0,00999 veces el brillo de B. Pero 0,00999 es aproximadamente 0,01, es decir una centésima, que es lo esperado, pues una diferencia de 5 magnitudes equivale a un factor de brillo de 100.

Nota: Hemos utilizado en la formula el valor de 2,512 por sencillez, el error producido es mínimo.

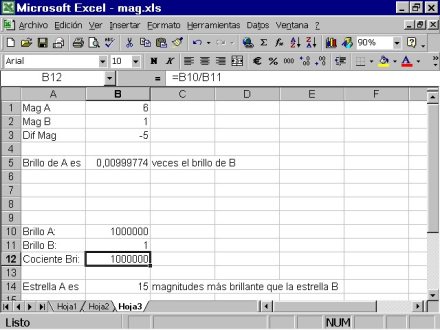
Ejemplos 6 y 7.

Cálculo Inverso

Podemos plantearnos el caso contrario. Sabemos que una estrella A es por ejemplo 10.000 veces más brillante que otra estrella B, ¿Cuál es su diferencia de magnitudes? Este caso es sencillo y lo podemos calcular mentalmente. Sabemos que 10.000 es igual que 100 · 100, y que cada factor de 100 corresponde a 5 magnitudes, así que la diferencia de magnitudes es de 10 (5+5). Esto es lo mismo que decir que 2,512¹⁰ = 10.000.

Pero si resulta que el brillo de la estrella A es 100.000 veces el brillo de B (osea que Brillo_A/Brillo_B es 100.000) es más difícil hacer el cálculo mentalmente. En este caso habría que encontrar un x tal que al elevar 2,512 a x, nos dé el número 100.000. Si lo planteamos matemáticamente quedaría así:

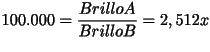
Lo mejor, para despejar x es tomar logaritmos:

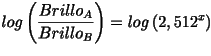
que equivale a

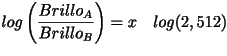
Pero el 2,512 en realidad es exactamente la raíz quinta de 100 o lo que es igual

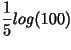, por tanto el log(2,512) que de forma más exacta es

será

, como el log(100) es 2, tenemos que el log(2,512) es exactamente

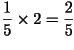. La fórmula queda por tanto como:

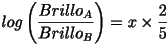
Si despejamos x tenemos que

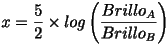
Qué resulta ser la archiconocida fórmula de Pogson. A veces tiene esta presentación:

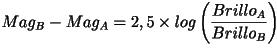
Entiéndelo mejor con hoja de cálculo

Ejemplo 7: En la misma hoja3, vamos a implementar la famosa fórmula de Pogson. Comenzando por los rótulos, en la celda A10 ponemos "Brillo A:", en A11 escribimos "Brillo B:", en A12 "Cociente Bri:", en A14 "Estrella A es", y en C14 escribimos "magnitudes más brillante que la estrella B". Vamos con los datos, en B10 ponemos 100000, en B11 ponemos 1000. Sólo faltan las fórmulas: en B12 escribimos "=B10/B11", que nos dará un resultado de 100 pues el brillo de la estrella A (100000) es 100 veces el brillo de la estrella B (1000). En la celda B14 ponemos la fórmula de Pogson "=2,5*log10(B12)".

Figura 4: Estrellas más brillantes
Nombre	Distancia (años luz)	Magnitud visual
Sol	-	-26,72
Sirio	8,6	-1,46
Canopus	74	-0,72
Centauro	4,3	-0,27
Arturo	34	-0.04
Vega	25	0.03
Capella	41	0,08
Rigel	1400	0,12
Procyon	11,4	0,38

Al dar ENTER veremos que el resultado es que la "Estrella A es 5 magnitudes más brillante que la estrella B", pues si una estrella es 100 veces más brillante que otra, decimos que es 5 magnitudes más brillante. Vamos a poner ahora en B10 el número 1000 y en B11 el número 10. Ahora tenemos también que el brillo de la estrella A es 100 veces el brillo de la estrella B, y comprobamos que la "Estrella A es 5 magnitudes más brillante que la estrella B". Fíjate que lo importante para saber las diferencias de magnitudes es conocer los cocientes de los brillos, no su valor real. La fórmula de Pogson no da la magnitud de una estrella conociendo su brillo. Sólo hace comparaciones entre dos estrellas, estableciendo las diferencias de magnitudes en función de los cocientes de sus brillos.

Si además conocieramos la magnitud de una de las estrellas, entonces sí podríamos calcular la magnitud de la otra. Veamos un caso: Si sabemos que la estrella B es de magnitud 18, y que otra estrella A brilla un millón de veces más que la estrella B, podemos mediante Pogson saber la magnitud de A. Metemos los datos en nuestra hoja de cálculo. En B10 ponemos 1000000, en B11 escribimos 1, y veremos que el resultado dice que la estrella A es 15 magnitudes más brillante que la estrella B. Cómo nos han dicho que la estrella B es de magnitud 18, la estrella A será de magnitud 3 (18-15).

Para mayor claridad en estos ejemplos hemos usado números redondos, múltipos de 10, pero puedes probar con cualesquiera brillo de estrellas. Si bien, entonces, te saldrán magnitudes con decimales.

Luis Salas López
Círculo Científico de Canarias
Editor asociado, Astronomía Digital
luis@astro-digital.com
http://www.cicican.org/
Gran Canaria, ESPAÑA

1998-2003 Astronomía Digital es una iniciativa de info.astro con la colaboración del Planetario de Pamplona. Se permite la reproducción total o parcial de los contenidos de la revista para uso personal y no lucrativo. Para el envío de artículos o cartas de opinión debe ponerse en contacto con la redacción mediante correo electrónico en digital@astro-digital.com o por carta a:
Astronomía Digital, Apartado de correos 271, 35080 Las Palmas de Gran Canaria (ESPAÑA).