

|
|
Predicción de la intensidad de las Leónidas (1999-2001)Ignacio Ferrín | Centro de Astrofísica Teórica, Universidad de los Andes (Venezuela)
Se ha desarrollado un nuevo método para predecir la intensidad de lluvias de meteoros, el cual aparece explicado en detalle en otra parte (Ferrin, 1999). En este trabajo se presenta un resumen del procedimiento sin formulas matemáticas, y de la predicción que se deduce de él. El método se basa en un gráfico (figura 1) que proporciona la densidad de partículas alrededor del cometa, y sobre el cual se dibujan líneas de igual intensidad de THZ (Tasa Horaria Zenital). El método se aplica a las Leónidas, resultando en las siguientes predicciones: Para 1999 la THZ será de unos 3500±1000. Para el 2000, sólo se puede poner los límites 5.000 > THZ < 20.000. Para el 2001 la THZ bajará a valores normales de 400±100.
Introducción.La lluvia de meteoros de las Leónidas ocurre cada 33 años aproximadamente, y ha dado espectaculares tormentas en 1799, 1833 y 1966. Pese a que la literatura contiene un enorme número de trabajos sobre esta lluvia, la característica general de ellos es que no se realizan predicciones "cuantitativas" sino "cualitativas" (Yeomans, 1981; Brown y Jones, 1993; Beech et al., 1997; Yeomans et al., 1996; Wu y Williams, 1992, 1995, 1996; Rao, 1998). La lluvia se origina por partículas de polvo emitidas por el cometa 55P/Tempel-Tuttle, el cual pasó por el perihelio en 1997. Esta incertidumbre de las predicciones ha llevado a Meisel, Director Ejecutivo de la Sociedad de Meteoros Americana (citado en Rao, 1998) a afirmar que "la predicción de lluvias de meteoros es notoriamente inconfiable. Nadie sabe como hacerlo apropiadamente".
El método.El método presentado en este trabajo pone a la predicción en buen pie, y se basa en la figura 1, la cual grafica Delta T vs P-E, donde P-E es la distancia de una partícula en la órbita del cometa a la Tierra, en su mínimo acercamiento, y Delta T es el tiempo transcurrido desde que pasó la Tierra por el nodo del cometa. Este gráfico ha sido hecho anteriormente por muchos autores. Lo nuevo de nuestro trabajo es que los puntos del gráfico no están etiquetados con el año de la observación sino con la intensidad de la lluvia, THZ. Así aparece la distribución del polvo alrededor del cometa, lo cual permite trazar líneas de igual concentración, y varias son mostradas en el gráfico. En otras palabras, por primera vez se presenta la distribución de polvo alrededor del cometa. Los datos graficados han sido tomados de Yeomans (1981), Rao (1998), Mason (1995) y Arlt (1998), y aparecen tabulados en Ferrin(1999).
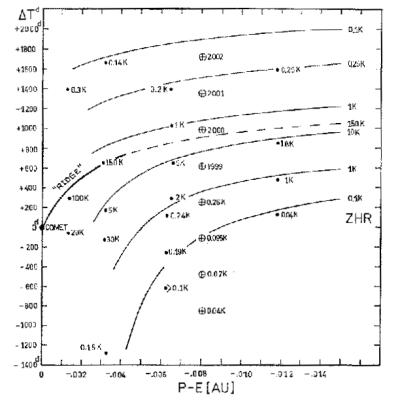
Distribución de partículas alrededor del cometa 55P/Temple-Tuttle. Los puntos han sido etiquetados con la intensidad de la lluvia, THZ. Los círculos con la cruz adentro marcan la posición de la Tierra en los diferentes años. Note la existencia de una región de mayor concentración de partículas sobre los puntos marcados con 150K y 100K.La THZ (Tasa Horaria Zenital --Zenital Hourly Rate, en inglés), es el número de meteoros registrado por un solo observador, con el radiante en el Zenit, y con un cielo de magnitud límite estelar MALE=6,5. Es claro que estas son condiciones ideales que difícilmente se logran por causa de cielos contaminados, cirros, amanecer, luz de la Luna, nubes, obstaculos visuales, radiante bajo en el horizonte, etc. Para calcular la THZ hay entonces que aplicar dos factores de corrección, los cuales a veces pueden ser muy grandes, y su producto aún mayor (¡hasta un valor de 10!). Por ejemplo la THZ de 86 registrada en 1994, es el resultado de observar 8 meteoros en 1/2 hora. En conclusión, "la THZ no es una cantidad observada sino deducida", y en consecuencia el número de meteoros observados es siempre menor que el dado por la THZ, y en ocasiones mucho menor. Los observadores deben ser conscientes de esto para no crear falsas expectativas. La cosa más interesante de la figura 1, es que muestra un "risco" o "colina" de elevadas concentraciones, y que pasa por dos puntos de intensidades 150.000 y 100.000 meteoros por hora correspondientes a 1966 y 1833. Debido a la falta de datos observacionales esta colina se pierde y se hace difícil extrapolarla hasta la posición tomada por la Tierra en 1999 y 2000 y marcada con un círculo con una cruz en su centro. Esta colina o risco es el lugar donde ocurren las grandes tormentas de meteoros de las Leónidas. Cruzar por ese punto hasta puede ser peligroso. Hemos identificado este risco con las "colas de polvo" estudiadas por Sykes et al. (1990, 1992) y encontradas detrás de todos los cometas periódicos. Estas colas se caracterizan por contener partículas de polvo muy grandes (del orden de 1 cm de diámetro), las cuales por ser tan grandes se mueven muy despacio (del orden de 4 km/s, en comparación con particular mucho mas pequeñas que se mueven a 20 km/s respecto al cometa). En otra parte (Ferrin, 1999) se presenta un cálculo completo de trayectorias de partículas eyectadas del cometa, las cuales muestran que en 1999 y 2000 la Tierra toca marginalmente la cola de polvo del cometa 55P. En consecuencia no ocurrirá una tormenta de meteoros, pero sí se espera una lluvia intensa. La mejor manera de apreciar esto es analizando la figura 2, la cual permite hacer predicciones cuantitativas.
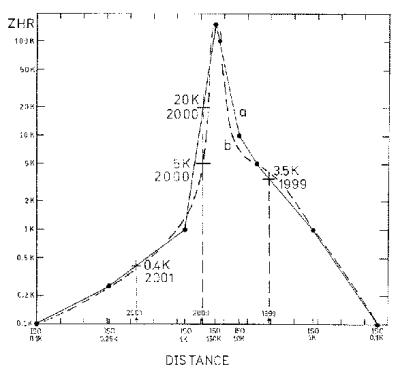
Perfil de la lluvia a lo largo de los puntos de la Tierra en la figura 1. Este perfil permite predecir la intensidad de la lluvia en los próximos años, lo cual esta hecho en el texto.
Predicción de la intensidad.La figura 2 muestra un perfil del polvo del cometa a lo largo de los puntos marcados para la Tierra en la figura 1. La figura 2 da THZ vs distancia a lo largo de los años. Allí se señalan las posiciones de la Tierra en 1999, 2000 y 2001. Se puede observar que hay un pico muy intenso (que corresponde a la cola de polvo estudiada por Sykes et al.), y que la intensidad decae muy rapidamente a ambos lados (como se espera físicamente). Una interpolación de los datos permite hacer predicciones "cuantitativas". Para 1999 se obtiene un valor de THZ=3.500±1000. Para el 2000 existe algo de incertidumbre, pues no sabemos con precisión la distribución exacta del polvo. Por tanto sólo podemos poner los limites 5.000 > THZ < 20.000. Para el 2001 la figura 2 muestra que la intensidad habrá bajado a niveles de THZ=400±150.
Predicción de la hora y fecha.Los gráficos mostrados arriba no contienen ningún indicio sobre la fecha y hora de la lluvia. Esta información puede ser deducida de los datos dados por IMO, la Organización de Meteoros Internacional. En su sitio web (http://www.imo.net) se dan las intensidades de la lluvia para cada año, como función de la longitud solar. Para 1998 el pico de THZ más intenso estaba situado en longitud solar 234,56°. Existen picos menores a mayores longitudes, pero estos no pueden ser la lluvia principal. De modo que si se repite el pico más intenso la fecha y hora de la lluvia será el 17 de noviembre de 1999 a las 8h 48m TU, o 17 de noviembre del 2000, a las 14h 42m TU.
Conclusiones.
Bibliografía
|