Astronomía Digital es la primera publicación electrónica de distribución gratuita en español orientada a la astronomía aficionada.

Todos los contenidos están disponibles de forma libre y completos en la Red para su lectura. Además, puedes leernos en papel imprimiéndonos gracias al formato PDF.

Astronomía Digital quiere llegar a todos los rincones de nuestro planeta donde se hable español.

Las variables UV Ceti y la distribución de Poisson

Siméon Denis Poisson.

Las UV Ceti son un caso extraño dentro del conjunto de las variables, siendo muy interesantes para los aficionados. Estamos acostumbrados a considerar que las variables experimenten un cambio de luminosidad en cuestión de meses, semanas o años, pero en este caso, el lapso de variación es del orden de minutos, como mucho de horas. Y además, el rango de dicha variación puede llegar a ser de seis magnitudes (es decir, unas 250 veces más brillante), aunque también nos encontramos con variaciones del orden de décima de magnitud.

Sin embargo, no es fácil encontrarse con una de estas erupciones mientras observamos, debido precisamente a su escasa duración. ¿Qué garantías tiene un observador con el ojo pegado al ocular, o con su maravillosa CCD, de cazar una de las erupciones y medir la variación de brillo? ¿Dónde se debe mirar?. Lo veremos después, pero antes, hablemos un poco de las UV Ceti.

Como ya hemos dicho, las UV Ceti son un tipo de variables. La mayoría de las que se conocen se corresponden con enanas rojas, muchas de ellas de la clase espectral M, y se encuentran por lo general en las asociaciones T Tauri. Como nota característica, en su espectro se pueden observar las rayas de emisión del Calcio y del Hidrógeno, rayas que aumentan de intensidad durante las erupciones.

Se pueden distinguir dos subtipos: las flare stars y las flash stars. Los flares, es decir, las fulguraciones, son directamente proporcionales en cuanto a duración respecto a la clase espectral. A una clase espectral más vieja, menos duración: en las K pueden durar casi dos horas, mientras que en las M5 no sobrepasan los veinte minutos, lo cual tiene una razón física en los modelos que se manejan en la que no vamos a entrar aquí. Su curva de luz, en general, es un tanto particular: tienen un crecimiento rápido de la luminosidad y un descenso más pausado.

Para hacerse una idea de lo que dichas erupciones representan para la estrella, es algo así como las erupciones solares, pero a una escala mucho mayor. Si, como se cree, la causa de las erupciones solares guarda relación con campos magnéticos ascendentes, puede suponerse, por analogía, que las erupciones de las UV Ceti tienen la misma causa, campos magnéticos, pero de mayor intensidad. Para otros astrofísicos, las causas van en el sentido de eyección de materia preestelar.

El interés del estudio de este tipo de estrellas se centra en los cúmulos estelares, pues es ahí donde podemos sacar conclusiones sobre la evolución estelar (téngase en cuenta que las estrellas de un cúmulo son de edad semejante).

Una vez enunciadas brevemente sus propiedades, vayamos al objeto de nuestro artículo: ¿cuál es la probabilidad de que en una sesión de observación sobre uno de esos cúmulos o agrupaciones nos encontremos con alguna fulguración?.

Para calcularla, planteemos dos hipótesis básicas: primera, que el número de erupciones por unidad de tiempo es igual para todas las estrellas, lo que se puede admitir sin demasiados problemas. Segunda, que las erupciones en un período dado son una variable aleatoria, que llamaremos X.

Con estas hipótesis, la probabilidad de que durante el tiempo t en que estemos observando la estrella sufra un número k de erupciones, sigue una distribución de Poisson de parámetro upsilon t, donde upsilon es la frecuencia de las erupciones. Bien escrito:

Analicemos lo que esta ecuación nos está diciendo con ayuda de unas gráficas. Es claro que upsilon t es el parámetro de la distribución (lo que habitualmente llamamos lambda), y nos refleja el número medio de erupciones que sufren las estrellas del grupo que estamos observando. Si hacemos variar esta lambda, obtenemos esto -nótese que no es continua, sino discreta-:

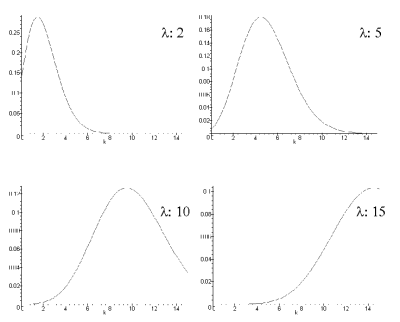
Distribución de Poisson.

Para visualizar mejor cómo varía la distribución de probabilidad según varía el parámetro, lo mejor es utilizar un programa como Maple V, de Waterloo Software, que nos permita realizar una animación.

En este programa el código queda como sigue:

restart;
with(plots):
f:=(E^(-lambda))*(lambda^k)/k!;
animate(f,k=0..10,lambda=1..15,frames=50,colour=red);

De lo que vemos se pueden extraer consecuencias más o menos obvias sobre el planteamiento de nuestro programa, a tenor de los datos de que dispongamos.

Un paso adelante consiste en calcular el número de estrellas fulgurantes que hay en nuestro grupo. Como se sabe, la distribución de probabilidad de Poisson de parámetro lambda tiene una esperanza de lambda, o lo que es lo mismo, la esperanza, el valor medio, del número de estrellas que han sufrido k fulguraciones es

donde N es el número de estrellas que habrán sufrido la fulguración.

Ahora bien, operando con las fórmulas (1) y (2), donde k toma los valores 0, 1 y 2, nos queda que:

En otras palabras, si conocemos el número de estrellas que ha sufrido una fulguración y el número que ha sufrido dos, sabemos que el número de estrellas de la agrupación o cúmulo que no han sufrido ninguna en el tiempo t dado es de n₀. Como conocemos el número de estrellas total, una simple sustracción nos da el número de estrellas fulgurantes. Y entonces, podremos compararlas con el número total, obteniendo conclusiones interesantes. Por ejemplo, en el caso de las Pléyades, aplicando las fórmulas a las observaciones realizadas hacia 1977 por V. Ambartsoumian, se deduce que unas 1.000 estrellas son eruptivas, es decir, prácticamente todas las del cúmulo. Entonces, ¿quiere esto decir que casi todas las estrellas del cúmulo son eruptivas?

No. El resultado es el descrito porque hemos supuesto que la luminosidad de las estrellas débiles y de las más brillantes sigue pautas iguales, lo que resulta no ser del todo cierto: las estrellas más brillantes tienen una disminución de luminosidad más rápida que las débiles (con lo que la probabilidad de detectarlas disminuye).

Un último apunte: dijimos al principio que una de nuestras hipótesis era que la frecuencia de las erupciones era igual para todas las estrellas consideradas. Podemos ser un poco más exigentes y desechar esta hipótesis,

con lo que obtendremos una cota inferior y superior del número de estrellas n₀ que no sufren ninguna fulguración.