Astronomía Digital es la primera publicación electrónica de distribución gratuita en español orientada a la astronomía aficionada.

Todos los contenidos están disponibles de forma libre y completos en la Red para su lectura. Además, puedes leernos en papel imprimiéndonos gracias al formato PDF.

Astronomía Digital quiere llegar a todos los rincones de nuestro planeta donde se hable español.

La Transformada de Fourier (I)

Una de las herrramientas matemáticas más útiles en ciencia es la transformada de Fourier (TF). Sus aplicaciones van desde la teoría de la señal hasta la Climatología, pasando por la Geografía e incluso la Biología. En relación a la Astronomía, hay muchos campos en los que es útil aplicarla. En este artículo y en su segunda parte trataremos de dos utilidades, referentes al campo aficionado: el análisis de series temporales y el tratamiento digital de imágenes. En esta parte hablaremos de la primera cuestión.

A pesar de que su formulación pueda parecer difícil a aquellos que no disfruten de una educación matemática superior, los rudimentos de la transformada de Fourier pueden entenderse perfectamente si se pone la atención suficiente. Hay dos fases: comprender qué es lo que se hace con una función -pues lo que se transforma son funciones-, visualizando de alguna manera el resultado; y después, ser capaz de utilizar esta técnicas por nosotros mismos, para lo que no se necesita un conocimiento más profundo: hay programas informáticos que hacen las operaciones por nosotros. Una tercera etapa consistiría en ser capaces de manejar la TF analíticamente, es decir, con sus expresiones matemáticas. Esta tercera etapa requiere de una base universitaria, pero no se pretende aquí que seamos capaces de diseñar nuestros propios filtros digitales, sino más bien que sepamos aplicar los que ya existen.

La transformada de Fourier es una operación que se realiza sobre funciones. Es decir, vamos a coger dos variables, la una dependiente de la otra -una función- y la vamos a convertir en otra variable que depende de una nueva -otra función-.

A la primera función la llamamos , o si preferimos, . Por definición, la transformada de Fourier de es:

¿Qué nos dice esta expresión? Es una especie de suma infinita -una integral- de la función de partida por el número elevado a la unidad imaginaria que multiplica a , a la nueva variable que decíamos, y a . Ya tenemos otra función, que depende de . Si aplicamos una conocida equivalencia que debemos a Euler -léase óiler-, se puede transformar lo anterior en:

Lo que hemos hecho es mirar de otra manera la exponencial elevada a un complejo. Ahora tenemos trigonometría, y es más fácil entender lo que se le hace a la función.

Lo que Fourier demostró en realidad es que cualquier función que cumpla una serie de condiciones razonables (las condiciones de Dirichlet) es equivalente a su transformada. Esta condiciones razonables se cumplen para la mayoría de las funciones con las que vamos a topar, por lo que se puede decir que la TF se puede aplicar casi siempre en el análisis de series temporales en Astronomía.

¿Y qué tiene de bueno que una función sea equivalente a su TF? Lo veremos con unos ejemplos.

Supongamos que tenemos la función , es decir, un polinomio sencillo, definido entre 0 y 1 por simplicidad. Si aplicamos la TF y dibujamos el resultado en el mismo plano en que dibujamos , nos queda el gráfico 1.

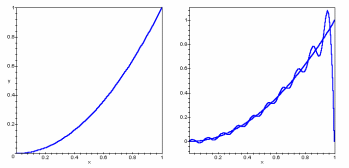
Figura 1.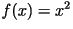

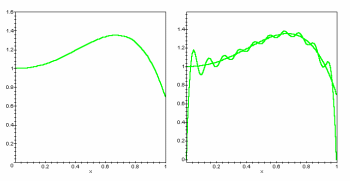
Figura 2.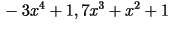

Hemos transformado una función en una suma de senos y cosenos que encaja bastante bien con ella. Hasta aquí, poco impresionante; la función era muy sencilla y hemos ganado poco.

Lo interesante viene cuando aplicamos la transformada a funciones más complejas. Para una función como en la gráfica 2, que ya no es tan trivial, tenemos que se sigue realizando un buen ajuste, transformando una expresión polinómica en una simple suma de senos y cosenos.

¿Y qué pasa si no conocemos la expresión analítica de la función de partida?. Llegamos al quid de la cuestión. No siempre vamos a tener polinomios, o a conocer como varía en función de . En las series temporales lo que tenemos es una tabla de valores, un número, a veces muy grande, de pares de números que se pueden reflejar en una gráfica.

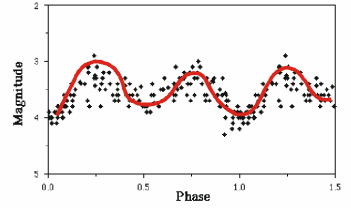
Figura 3. Curva de luz de una estrella variable periódica.

Pero no sabemos qué sucede si tomamos un valor para la que no esté en la tabla. Y precisamente, eso es lo que nos interesa: saber qué pasará entre los valores que tenemos -interpolar- o, más interesante, más allá de ellos -extrapolar-.

Si hemos realizado 200 observaciones de una estrella variable irregular, queremos saber qué brillo va a tener el miércoles de la semana que viene. Si hemos calculado el número de Wolf, querríamos saber cuál va a ser el mes o el año que viene. Si hemos accedido a la web de la NASA y nos hemos traído una tabla de temperaturas en Marte, querríamos ver qué pauta sigue su variación para establecer un modelo. Hay que apresurarse a decir que la TF no resuelve del todo estos problemas: es un medio de aproximarse a ellos, mucho más eficaz que otros.

Por ejemplo, en el caso de una variable como la del gráfico 3 podríamos intentar realizar un ajuste polinómico. El error que se comete en el mejor de los casos, con un polinomio grandecito de grado 6, es muy superior al que se comete calculando la serie de Fourier (el ajuste con polinomios puede hacerse con programas comunes, como Microsoft Excel o StarOffice). Si lo intentamos con U Geminorum, con una gráfica como la de la figura 4, no vamos a tener tanta suerte para encontrar un buen ajuste polinómico (nótese que las dos gráficas son diferentes). Necesitamos algo operativo y más o menos automático.

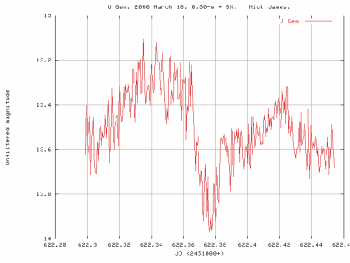
Figura 4. Curva de luz de U Gem.

El cómo se calcula la TF de Fourier a partir de datos sueltos, y no de una expresión analítica, no es complicado si no se entra en formalismo matemático. En síntesis, lo que se hace es cambiar la integral (que podemos ver como una suma infinita a lo largo de una recta continua) por una suma infinita a lo largo de una recta que llamamos discreta, o sea, discontinua. A eso se le llama serie. Se habla entonces de la serie de Fourier de la función y de la tranformada discreta de Fourier (TDF).

La serie de Fourier tiene infinitos términos, de los cuales en la práctica sólo podemos calcular unos pocos. Lo que sucede, a grandes rasgos, es que según se añaden nuevos términos se gana en precisión, es decir, la TDF se acerca más a la función origen. A éstos sumandos se les llama en la jerga armónicos. Es decir, si decimos que la TDF de la función es con tres armónicos, esto quiere decir que hemos cortado a partir del cuarto sumando. En la gráfica 5 hay tres representaciones además de la de la función, cada uno de los cuales tiene más armónicos que el anterior. Según aumentamos el número de sumandos, se ve cómo nos ajustamos mejor a la función.

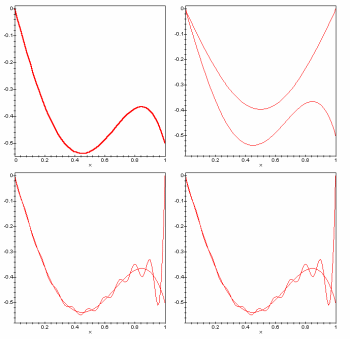
Figura 5. Gráfica con sus ajustes sucesivos.

¿Cómo podemos calcular la TDF? Los programas de cálculo simbólico, como Matlab o Maple la incluyen, por supuesto. Paquetes estadísticos, como el SPSS la poseen también. Si nos gusta programar, podemos intentarlo nosotros mismos: el código está en el gráfico 6 en forma de función de C++ (hay una versión más rápida para realizar el cálculo, al Transformada Rápida de Fourier, que veremos en otra ocasión). Se trata de un programa que realiza las operaciones sobre imágenes, al que sacaremos mayor partido en la segunda parte de este artículo, pero puede ser utilizado para ajustar series temporales con pequeñas modificaciones.

Para finalizar esta primera parte, señalar algunas actividades que se pueden realizar. En la página Web del SIDC, entre otros lugares, se pueden encontrar registros históricos del número de Wolf. Cualquiera puede bajarse los datos y empezar a trabajar con ellos. En el Grupo Universitario de Astronomía de Valladolid estamos estudiando en este momento las relaciones entre la variación de éste y diversos ámbitos geográficos, como el clima. Se ha visto que, en algunos aspectos, el análisis de Fourier es útil. En otros trabajos, como el análisis de las temperaturas medias mensuales en diversos puntos del territorio, se ha demostrado que es el método más satisfactorio de ajuste.

   Rutina en C++ para el cálculo de la
   transformada de Fourier de imágenes

   Francisco J. Tapiador. 24 de abril de 2000
   Método clásico. Lento pero fácil de comprender
   Sólo para imágenes cuadradas


#define PI 3.141593
#define xydim T
// T es un valor fijo definido por el usuario.
// Puede también pasarse a la función.

void Fourier1(imag, freal, fimag) {
// recibe 'imag' como una matriz bidimensional en
//   la que guardan los valores 'x' e 'y'
// 'freal' la parte real del resultado y 'fimag'
//   la imaginaria
double imag[][xydim];
double freal[][xydim];
double fimag[][xydim];
double phi, sum1, sum2;

for (int i = 0; i -- xydim; i++)
  for (int j = 0; j -- xydim, j++) {
    sum1 = 0;
    sum2 = 0;
    for (int x = 0; x -- xydim; x++) {
      for (int y = 0; y -- xydim, y++) {
        phi = 2 * PI *(i * x + j * y) / xydim;
        sum1 = sum1 + imag[x][y] * cos(phi);
        sum2 = sum2 + imag[x][y] * sin(phi);
      }
    }
    freal[i][j] = sum1 / xydim;
    fimag[i][j] = -sum2 / xydim;
  }
}